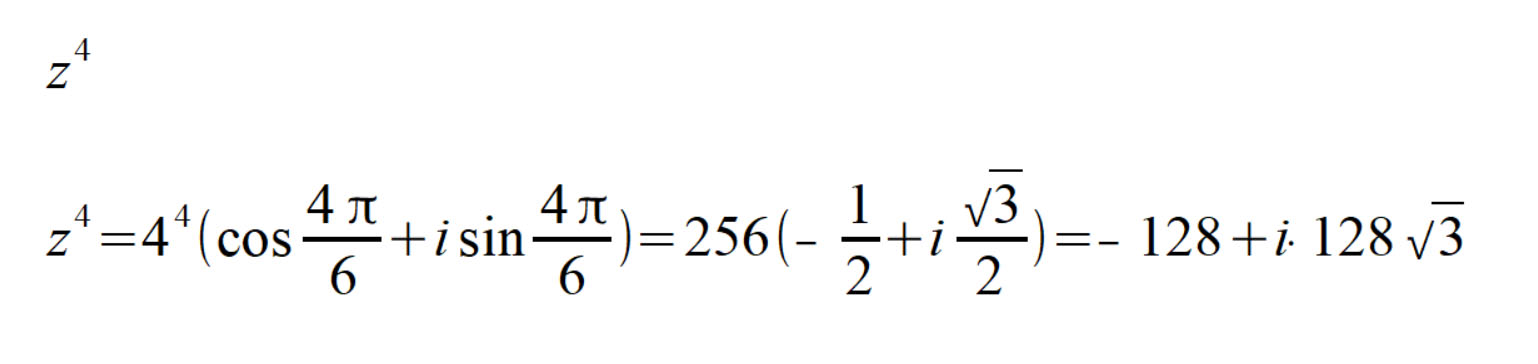Рассмотрим случай, когда комплексное число необходимо возвести в степень. Как правило, комплексное число задано в алгебраической форме, к примеру:
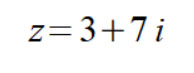
Необходимо возвести во вторую степень комплексное число z.
Поэтому первым делом избавляемся от алгебраического представления и приводим наше число к тригонометрическому виду:
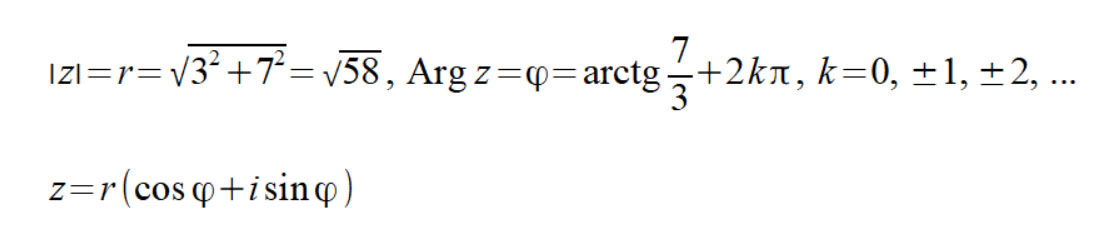
Формула Муавра утверждает, что степень
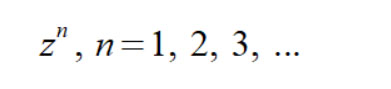
комплексного числа z равна
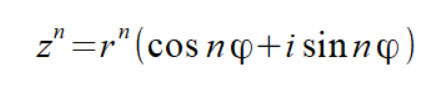
Применяем формулу Муавра:
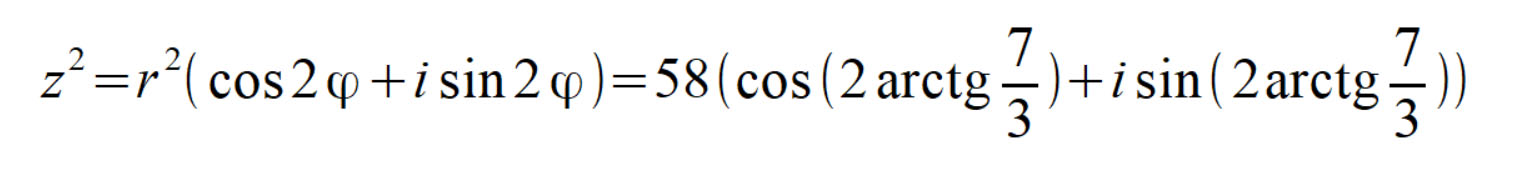
По большому счету, что значит возвести комплексное число в степень? Это умножить комплексное число само на себя n раз. На мой взгляд, формулу Муавра целесообразно использовать в случае, когда степень n > 2. В ином случае, когда n = 2, можно поупражняться в умножении комплексных чисел как обычных алгебраических двучленов, рассмотренных в статье ранее. А в целом, эта формула работает для любой степени.
Пример 1. Возвести в четвертую степень комплексное число
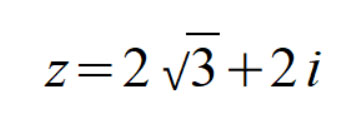
Сначала разберем структуру исходного комплексного числа, которое необходимо возвести в степень. Запишем, чему равно значение его действительной и мнимой части:
.
Найдем модуль и аргумент комплексного числа:
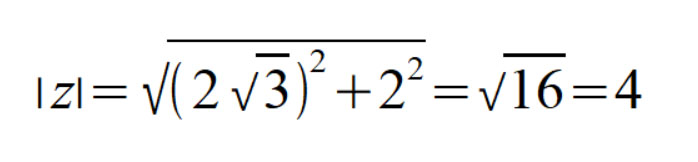
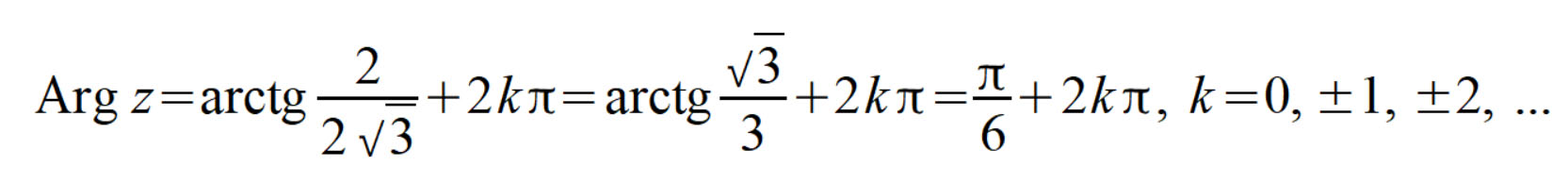
Запишем тригонометрическое представление комплексного числа:
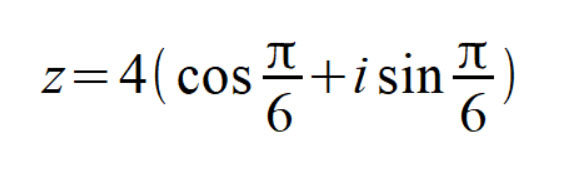
Теперь, используя формулу Муавра, найдем